Quantum Go Fish — это лишь одна из многих математических игр в последней книге Бена Орлина Математические игры с плохими рисунками.”>

Из тысячи игр, с которыми я столкнулся, работая над своей книгой, Математические игры с плохими рисунками, только один из них по-настоящему напугал меня. Это пальчиковая игра. Но поверьте мне: это самая сложная интеллектуальная игра для пальцев, когда-либо придуманная человечеством — нечто среднее между логической головоломкой, импровизированной комедией и коллективной галлюцинацией, в которую играют с самой странной колодой карт, которую вы когда-либо видели ( или не видел). Держите аспирин наготове.

Как играть

Что вам нужно? Где-то от трех до восьми игроков. Каждый начинает игру, подняв вверх четыре пальца. Это «карты» в колоде.

Какова цель? Есть два способа выиграть:

1. Докажите, что у вас четыре карты одной масти.
2. Точно укажите, какие масти есть у каждого игрока в руке.

Каковы правила?

Начать, никто не знает мастей своих (или чужих) карт. Все есть тайна. Мы знаем только, что есть четыре карты одной масти и столько мастей, сколько игроков.

В свой ход выберите другого игрока и спросите их, есть ли у них карты определенной масти. Первый, кто сошлется на новый костюм, придумает для него глупое название. Note это вы можете запросить только тот костюм, который у вас уже есть; таким образом, запрашивая Единорогов, вы отдаете одну из своих пока неизвестных карт на роль Единорога.

Спрашиваемый игрок может ответить одним из двух способов:

• «Нет, у меня их нет». Таким образом, все их карты должны принадлежать другим мастям.
• “Да, вот один.” В этом случае дают ровно одна карта запрашивающему игроку. Другие их карты остаются загадкой (и могут принадлежать или не принадлежать той же масти).

Иногда это решение будет вынужденным. Например, если вы уже обязались есть редис, и я прошу у вас редис, вы должны дать мне один. Если это не принуждение, спрошенный игрок может ответить так, как пожелает.

Выиграть можно двумя способами:

• В конце вашего хода, укажите, какие именно карты должны быть у каждого игрока.
• В конце вашего хода, докажи, что у тебя четыре карты одной масти.

Однако, если возникает парадокс — это означает, что игроки вместе имеют пять или более карт одной масти, и никто не уловил ошибку в то время, — тогда что-то пошло не так, и все проигрывают.

Пробный раунд

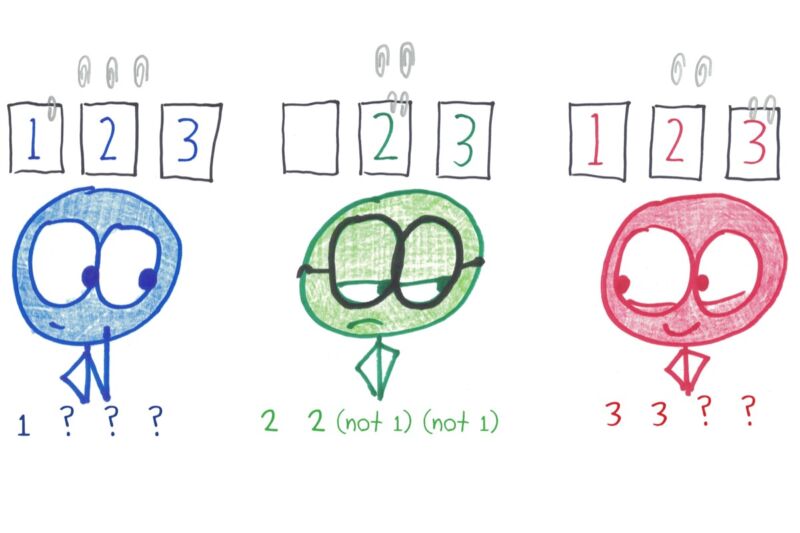
Три игрока начинают с 12 картами: по четыре каждой из трех разных мастей. Никто не знает, какие карты у них (или у кого-либо еще) есть.

Ся идет первой и спрашивает: «Яэль, у тебя есть нарвалы?» Яэль предпочитает отвечать: «Нет».

Следующей идет Яэль и спрашивает: «Зои, у тебя есть какие-нибудь сомнения?»

Зоя решает ответить: «Да».

В результате у Зои остается три карты, а у Яэль — пять. Из них два должны быть Скрупулями: одно подразумевается, когда вы просите, и одно получено от Зои.

Следующей идет Зои и спрашивает: «Яэль, у тебя есть сомнения?»

Яэль может испытать искушение сказать: «Нет». Но это привело бы к парадоксу, разрушающему игру. У Яэль есть три карты, которые не являются нарвалами; если они и не Квалмы, то они, должно быть, Скруплы. Это дало бы Яэль пять совести, что невозможно.

Поэтому Яэль должна сказать «Да» и передать Зои Квалм.

Следующей идет Ся и спрашивает Зои: «У тебя есть нарвалы?»

Умный ход. Если Зоя скажет «нет», то ни у Яэль, ни у Зои не будет нарвалов. Таким образом, Ся получит их всех и сможет претендовать на победу. (Некоторые игроки запрещают начинать с четырьмя картами одной масти; по этому правилу Зоя должна была бы сказать здесь «да».) Вместо этого Зои говорит «Да» и дает нарвала Ся, у которого теперь есть как минимум две карты. Нарвалы.

Яэль на следующем повороте спрашивает: «Ся, у тебя есть сомнения?» Это означает, что одна из оставшихся карт Яэль должна быть третьим Qualm.

Ся решает ответить «Да» и дает последний Qualm Яэль. Теперь говорят обо всех Qualms. Более того, поскольку последняя карта Яэль не может быть Нарвалом и больше не может быть Квалмом, это должно быть Скрупл.

Следующий ход падает на Зои, которая спрашивает: «Ся, у тебя есть сомнения?»

Это означает, что последней картой Зои является Scruple. На самом деле, это последний Скрупл, а это значит, что у Ся его быть не может. Почему Зоя вообще удосужилась спросить?

Потому что, учитывая все Сомнения и сомнения, Зои знает, что оставшиеся карты Ся — это Нарвалы. Декларируя и объясняя это знание, Зои выигрывает игру. (Ся, несмотря на то, что закончил игру со всеми четырьмя нарвалами, начал только с тремя, а позже получил одного от Зои.) Легко, как в воскресенье утром, верно?